比例のグラフは簡単に書ける!?
こんにちは!今回お話しするのは中1で学習する「比例のグラフ」です。
比例のグラフはどうやって書くのか、思っている以上に簡単だということをお伝えします。
グラフが書けるために

大前提ですが。比例のグラフは「原点」を通ります。原点というのは(0,0)の部分(xの座標, yの座標)ですね。
グラフが書けるためには2つのパターンがあります。
1つは「xとyがわかること」、もう1つは「傾き(変化の割合)がわかるとき」です。
これだけ言っても意味が分からないかと思いますのでそれぞれのパターンをお話しします。
xとyがわかるとき
例題を挙げつつお話ししていきます。まずは、xとyがわかるときです。
問:(2,6)を通る比例の式を求めなさい。
ここでいう(2,6)というのは座標です。
つまり、X=2、Y=6だと思えばいいわけです。
y=a𝒙
これが比例の式なので、XとYを代入します。
6=2a
2a=6
両辺を2で割ると
a=3
最後に元の式に代入すると、
y=3𝒙
になります。
ちなみにこの式の場合、(1,3)、(2,6)、(3,9)を通る直線を書けばいいということになるので、xとyの数値さえわかれば解けるのです。
問1:(3,8)を通る比例の式を求めなさい。
X=3、Y=8を代入すると、
8=3a
3a=8
両辺÷3したらいいので、
a=8/3
最後に元の式に代入すると、
y=8/3𝒙
になります。
問2:X=2, Y=6を通る比例の式を求めなさい。
X=2、Y=6を代入すると、
6=2a
2a=6
両辺÷2したらいいので、
a=3
最後に元の式に代入すると、
y=3𝒙
になります。
傾きがわかるとき
問:傾きが3のときの比例の式を求めなさい。
傾きというのは、
y=a𝒙
でいうaの部分になります。別名は変化の割合ですね。ということは、傾きがわかったら式が求められますよね。
y=3𝒙
以上です。
先ほどと同じように(1,3)、(2,6)、(3,9)を通る直線を書けばいいということになるので、傾きさえわかれば式はわかってしまうのです。
問1:傾きが2のときの比例の式をもとめなさい。
y=2𝒙
問2:傾きが10のときの比例の式をもとめなさい。
y=10𝒙
変化の割合の求めかた
最後に変化の割合です。傾きの=変化の割合ですよという話です。
xとyを代入する方法をお伝えしましたが、もう1つの方法として変化の割合から式をつくるという手段があります。
変化の割合は
yの増加量/𝒙の増加量で求めることができます。
増加量とはなんでしょう。
例えば、xが2⇒6、yが3⇒9に増加したとしましょう。するといくら増加しましたか?というのが増加量です。
この場合、xについては6-2=4、yについては9-3=6ということになるので、
yの増加量/𝒙の増加量にあてはめると、6/4=3/2
よって、変化の割合=傾きになるので、
y=3/2𝒙ということになります。では、練習してみましょうか。
<練習>
①変化の割合が5のとき、比例の式を答えなさい。
変化の割合=傾きだから、y=5x
②xが3から6に、yが4から8に増加したときの比例の式を答えなさい。
yの増加量/𝒙の増加量にあてはめると、8-4/6-3=4/3
よって、y=4/3𝒙
グラフは分母と分子から考える!
では式が求まったので、x=1のとき、x=2のとき・・・みたいに計算しないといけない!?わけではありません。もっと簡単です。
それが、分母と分子の数だけ動くということです。さきほどあげた
y=4/3𝒙の場合、x軸の方向に+3、y軸の方向に+4進んだグラフになります。逆にこの分数に-がついて、
y=-4/3𝒙
の場合、x軸の方向に-3、y軸の方向に+4進んだグラフになります。そのため、x=1のとき、x=2のとき・・・みたいに計算しなくてもx軸の方向に+3、y軸の方向に+4進んだところに点、またそこからx軸の方向に+3、y軸の方向に+4進んだところに点というようにして書けばいいのです。
しかも、比例のグラフは必ず原点(0,0)通るので、もう1か所点がわかれば直線が書けますね!
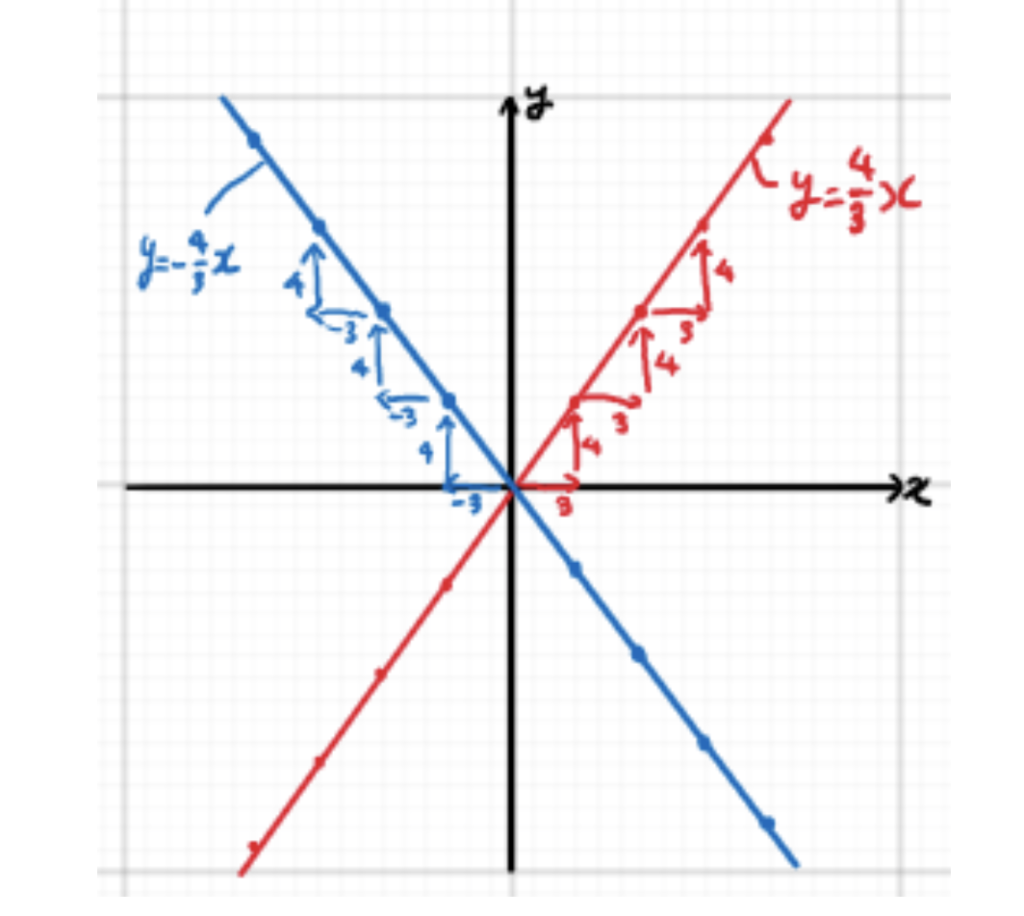
<ルールのまとめ>
①分数がプラスの時
分母の数だけ右に進み、分子の数だけ上に進んだところに点を書く
②分数がマイナスの時
分母の数だけ左に進み、分子の数だけ上に進んだところに点を書く
まとめ

比例のグラフは非常に簡単に書けます。
まず、2~4でお話ししたようにいろんな求め方があり、そしてそこで式を求めることができれば、5の方法でグラフを書くことができます。
問題では様々なヒントが与えられます。2のパターンだったり3のパターンだったり…
だからこそ、どのパターンでも式が求められるようにすることがグラフを書くために必要な力となります。
今後学習する関数でもグラフを書くという問題は出てきます。今の段階でグラフを書くことに慣れていきましょう!



