こんにちは!今回お話しするのは中1で学習する「反比例」です。
反比例ってちょっと難しいなぁなんて思う人もいるかもしれませんが、そんなことはない!比例と同じように簡単にわかるのが反比例です。
反比例の形を知る
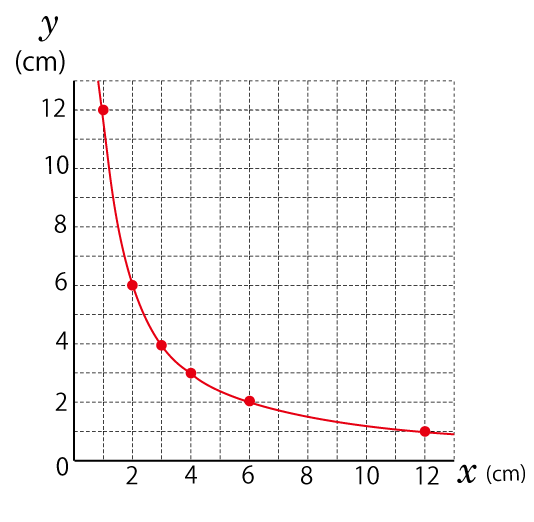
2つの方法で比例・反比例を見分けることができます。
1つ目は、「表で見分ける」
2つ目は、「式で見分ける」
今回は反比例だけを見ていきましょう。
①反比例の表
まず皆さんには表を見てもらいます。
| 縦の長さ | 1 | 2 | 3 | 4 | 5 | 6 |
| 横の長さ | 24 | 12 | 8 | 6 | 4.8 | 4 |
下の段の数字が右になればなるほど小さくなるという表ですね。このように片方の数字のみが増えていくものを「反比例」というのです。
つまり、反比例=片方の数字が大きくなれば、もう一方の数字は小さくなっていくなんですね。
<練習>問:次のうち反比例はどれ?
(1)100円のペンをX個買ったときの値段Y円の関係
(2)横の長さXcm、縦の長さYcmの時の長方形の面積が24cm2の関係
(3)毎秒Xmで進む電車がY秒走った時の距離が330mの関係
(4)毎分10mで進む人がX分歩いた時の距離がYmの関係
<(1)の解説>
1個買ったとき、100円×1個=100円(=Y)
2個買ったとき、100円×2個=200円(=Y)
3個買ったとき、100円×3個=300円(=Y)
というようにXの数値が増えるとYの数値も増えるので比例!
<(2)の解説>
横が1cmのとき縦は24cm (24÷1=24)
横が2cmのとき縦は12cm (24÷2=12)
横が3cmのとき縦は4cm (24÷3=4)
というようにXの数値が増えるとYの数値が減るので反比例!
<(3)の解説>
毎秒1mのとき330m (330÷1=330)
毎秒2mのとき165m (330÷2=165)
毎秒3mのとき110m (330÷3=110)
というようにXの数値が増えるとYの数値が減るので反比例!
<(4)の解説>
1分のとき距離は、毎分10m×1分=10m(=Y)
2分のとき距離は、毎分10m×2分=20m(=Y)
3分のとき距離は、毎分10m×3分=30m(=Y)
というようにXの数値が増えるとYの数値も増えるので比例!
よって、反比例になるのは(2)(3)ですね。
②反比例の式
反比例には式があります。
長方形において
| 𝒙 | 縦の長さ | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 横の長さ | 24 | 12 | 8 | 6 | 4.8 | 4 |
反比例の式を考えるために、上の段を𝒙、下の段をyとしてみましょう。
縦の長さが1、横の長さが24ということで、面積は24
縦の長さが2、横の長さが12ということで、面積は24
縦の長さが3、横の長さが8ということで、面積は24
つまり、縦の長さ×横の長さしたら24になるんです!文字で置くと、
𝒙y=24
になるんです。
そう、これが反比例の式。
𝒙y=a
この形になるものが反比例になります。ただし、反比例は両辺を÷𝒙して、
y=a/𝒙
この形で教えられることが多いので、両方の形を知っておきましょう!
反比例の式を求める
では、反比例の式を求める方法をお話ししましょう。
大きく分けて2つあります。
問:(2,6)を通る反比例の式を求めなさい。
(2,6)はグラフの座標を表し、𝒙=2、y=6
と思ってもらえればいいです。
反比例の式は2種類書きましたね。
①𝒙y=a
②y=a/𝒙
この2種類ですね。では、それぞれに代入します!
①2×6=a
a=12になるので、𝒙y=12になります。
②6=a/2
右辺の2が邪魔なので、両辺に×2をしましょう。すると、
12=a
になるので、
y=12/𝒙
となるわけです。もちろんを両辺÷𝒙すれば、y=12/𝒙になるので全く同じものです。
自分が楽だと思う方法をうまく使って計算してみましょう!
<練習>
① (3,6)を通る反比例の式を答えなさい。
★3×6=a
a=18
になるので、𝒙y=18になります。
★6=a/3
右辺の3が邪魔なので、両辺に×3をしましょう。すると、
18=a
になるので、y=18/𝒙となるわけです。
② (5,20)を通る反比例の式を答えなさい。
★5×20=a
a=100
になるので、𝒙y=100になります。
★20=a/5
右辺の5が邪魔なので、両辺に×5をしましょう。すると、
100=a
になるので、y=100/𝒙となるわけです。
まとめ

いかがでしたか?反比例というものは難しくないわけです。だって、𝒙y=aの形わかっていればもう勝ちですもんね。
反比例の式と言われるとy=a/𝒙の形で答えることが多いので、もちろんこっちも知っておかなければなりませんが、それでもxとyを代入してしまえばとにかくaがわかるので簡単に解けるのです。
反比例の勉強法というよりかは、今後必要な力、比例でも必要な力である、「代入」をうまく使って解けるようになることこそが一番の反比例の勉強法なのです。



