今回扱うのは「1次方程式」です。
みなさんは新しく「方程式」という内容を学習していきますが、この方程式は数学において非常に非常に役に立つものですから、ぜひ身につけていきましょうね!
等式のルール

等式にはルールが存在しています。そのルールをまずは覚えましょう。
①方程式とは
方程式とは、式を=で表したものです。イメージは=の左と右が全く一緒ですよ~という役割です。
最終的には、x=○○という形で答えを出します。この答えを「解」といいます。
②等式ルール集
【A】両辺(=の左と右)に同じ数を「+」「-」「×」「÷」しても=になる。
【B】左辺と右辺を入れ替えても=になる
めっちゃシンプルですね。これをうまく使って解くのか方程式なのです!!
ではどんな時に使うのでしょうか?
問:2X/5=4の解を求める。
この場合、左辺の5がまず邪魔なわけです。そのため、両辺に5をかけてあげます。
すると、2X=20になりますね。最後に左辺の2が邪魔ですから、両辺を2で割ります。X=10になって解が求まります。
移項とは
移項とは、左辺にあるものを右辺、右辺にあるものを左辺に動かすということです。ですが、難しい話ではありません。先ほどのルールを思い出せばいいのです。
問:2X+8=4X−12の解を求める。
この時にやってほしいこと。それは左辺にXをすべて持ってくること!でもじゃあ4Xをそのまま左辺に持っていこう!はダメです。
なぜかと言えば=にならなくなるんですよね。右辺から4Xを引いてしまうのであれば、左辺からも4Xを引かないといけません。
2X−4X+8=4X−4X−12
−2X+8=−12
次は8ですね。左辺から8を引くのであれば、右辺からも8を引かなければなりません。
2X+8−8=−12−8
−2X=−20
するとルールで学んだことを使います。左辺の-2が邪魔なので、両辺を-2で割ってあげればいいんですね。すると
x=10
よって、解は10ということになります。
じゃあ、移項ってこんなに面倒なのかというと、これは本来の仕組みを説明しただけで、実際は「符号が入れ替わる」と思ってくれれば問題ありません。
4xを左辺に持っていくのであれば、左辺に-4xを書きます。
逆に8を右辺に持っていくのでがあれば、右辺に-8を書きます。
ここまでくると同じです。
x=10
よって、解は10ということになります。
方程式の解き方

はっきり言いますと、方程式の解き方はもうお伝えしました。ルールや移項を使えば解けるわけです。しかし、それだけではできない計算もあるので、その部分をお話しします。
<かっこのある式>
問:3(X+4)=20−X
たとえばこんな問題が出てきたらどうしますか?まず、()を外すということが必要になります。そこで、「分配法則」というものを使います。

分配法則は、イラストを見てもらったらわかったかと思いますが、3をxにも4にもかけるのです。
このように、()の直前に数字や文字がついているときは分配法則を使います。
<小数を含む式>
問:−0.2X+5=−5+0.8X
小数が入ってきましたが、どうしましょうか?これは、「小数を整数にする」ことを優先してやります。
どうすれば整数になるかと言うと、両辺に10倍してあげれば整数になりますね。(0.01等の場合は100倍しますね)

<分数を含む式>
実は最初の例で挙げました。
2X/5=4
この例ですね。この場合は、「分数を整数にする」ことを優先してやります。

比例式の解き方

最後に「比例式」を扱います。比例式とは、「比」を活用した方程式です。
例えば、
a:b=c:d
という形を比例式と言いますが、これはa:bの比とc:dの比は同じだよという意味になります。
問)2:X=4:6
比の計算のポイントは「内内外外」です。内側同士をかける、外側同士をかけるという計算方法をします。
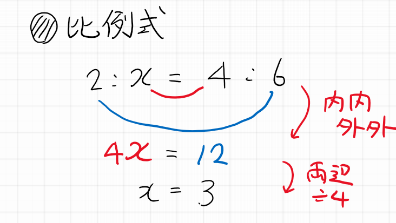
計算式はイラストにもあるように、
4x=2×6
4X=12
両辺4で割ればいいから、
X=3
という答えになります。実際に考えてみると、2:3=4:6というのは、4:6を簡単にすれば2:3になるので、イコールと言えるわけですね。
比はとにかく「内内外外」なのです。
まとめ

方程式は、いかに「ルール」「移項」をしっかりと使ってX=の形にできるかを
考えればよいのです。X=にしようと思ったら、何を足したり、引いたり、かけたり、わったり・・・なんてことを考えながら計算を進めていってください!
そして比例式は何度も言いますが、「内内外外」これだけで十分です。()が出てきても分配法則を使えばいいですからね~
方程式は2年生で連立方程式、3年生では2次方程式として応用版が出てきます。
ここでしっかりと方程式に慣れておきましょう!



