
小学生の算数で「比例・反比例」ではグラフが登場し、自分でグラフを書いたり、イメージすることが必要なため、難しいと感じてしまうお子様が多いです。
実際、大人の人も小学校の時に習った比例・反比例をちゃんと説明することは難しいかもしれません。
そこで、この記事では小学生でもしっかり理解できるように「比例・反比例」をわかりやすく解説していきます。
【小6算数】「比例」を勉強する時のポイント

比例とは、2つの数値のうち一方が0なら0で、一方が増えていくともう片方の数値も大きくなっていくものです。
また、2つの変数xとyがあるとき、次の式で表すことができます。
y=ax
上記の式の場合は、yはxに比例するといい、小学校の場合は針金の長さと重さや縁の直径と円周の長さなどが問題になります。
ちなみに、aは比例定数といい、yがどのくらいの割合で増えていくのかを表した文字です。
| 針金の長さ | 1m | 2m | 5m | 8m | 10m |
| 針金の価格 | 100円 | 200円 | 500円 | 800円 | 1000円 |
針金1mが100円だとすると、2mは200円、5mは500円と価格が上がっているのを上記表にまとめました。
この表をみてわかるように、同じ倍率で数値が増加していますね。これが比例の関係であるといいます。
比例のグラフ
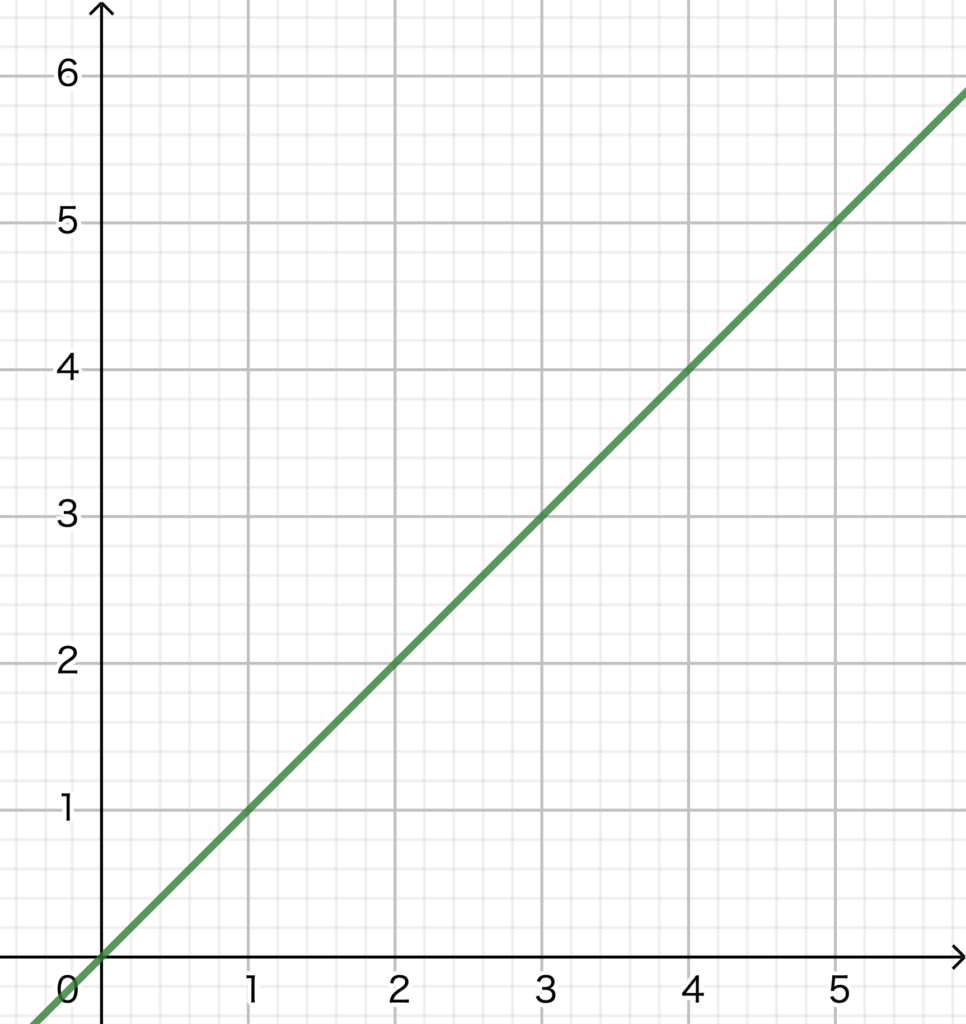
比例はグラフを描くとイメージしやすいので、上記比例定数a=1の時のy=xの比例関係のグラフになります。
グラフを見ると、比例する場合は数が原点を通り一直線で変化していき、xの値が2倍、3倍になるとyの値も2倍、3倍になっていますね。
このように右に行くにつれて上も伸びていく右肩に直線で上がっていくものが比例のグラフで、比例かどうかの見分け方は、y÷xをしてどこでも比例定数が同じ値になった場合は比例で、それ以外の場合は比例ではありません。
上記グラフの場合は、
y=1の時x=1なので、 1÷1=1
y=5の時x=5なので、 5÷5=1
のように全て比例定数の1が答えになります。
このように、xの値の変化量とyの値の変化量が常に一定の比例定数aで推移する関係のことが比例です。
【小6算数】「反比例」を勉強する時のポイント

それでは今度は反比例を説明していきます。反比例は比例に反がついている言葉通り、比例の逆です。
一方が2倍、3倍、4倍と増えると、もう片方の数値が1/2倍、1/3倍、1/4倍と小さくなっていく関係性の数値です。
また、2つの変数xとyがあるとき、次の式で表すことができます。
y=a/x
上記の式の場合は、yはxに反比例するといいます。aは比例定数といい、yがどのくらいの割合で減っていくのかを表した文字です。
反比例のグラフ
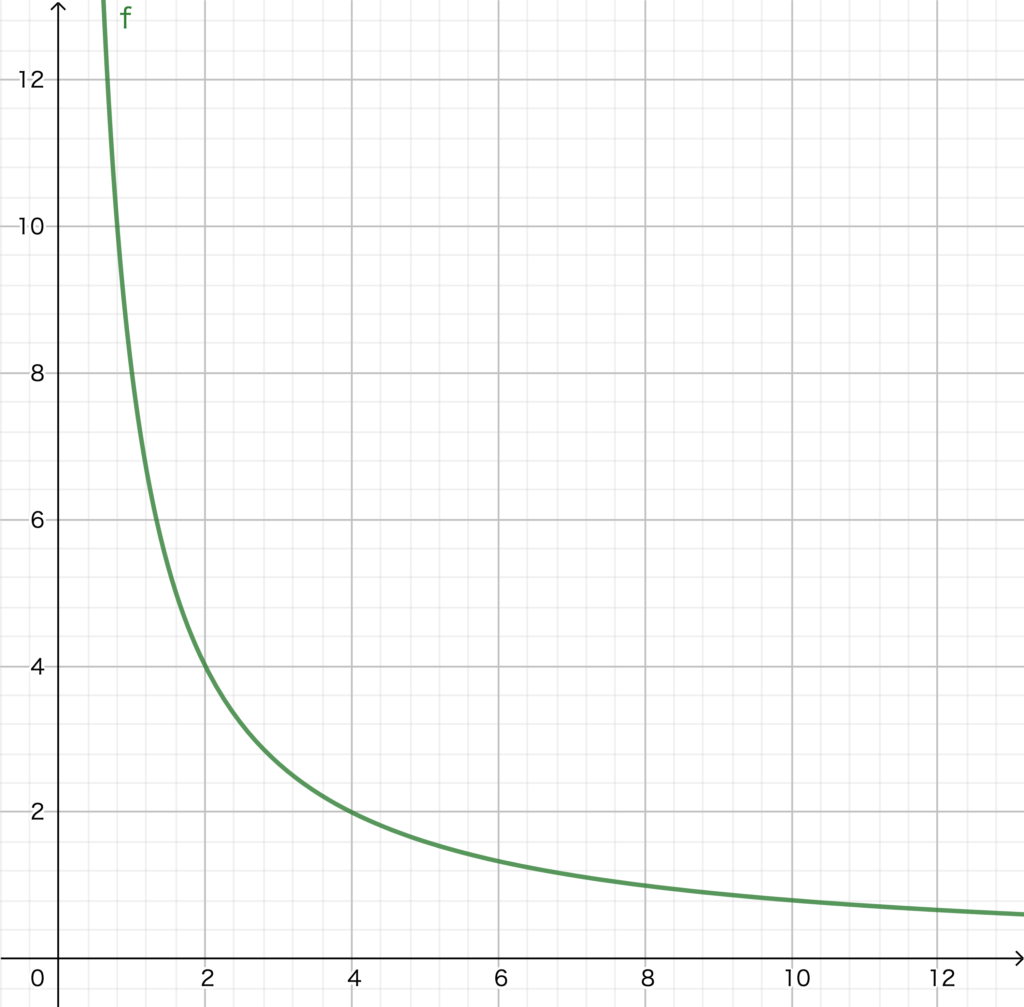
反比例もグラフを描くとイメージしやすいので、比例定数a=8の時の反比例の関係が上記グラフです。
反比例する場合のグラフでは、比例と異なり原点を通らずに双曲線になり、xの値が2倍、3倍になるとyの値は1/2倍、1/3倍になっていることが確認できますね。
反比例のグラフはわかりにくいですが、xの値の変化量とyの値の変化量を掛け合わせた時に常に一定の比例定数aで推移する関係のことを反比例といいます。
上のグラフの場合は、
x=1の時y=8なので、1×5=8
x=2の時y=4なので、2×4=8
x=8の時y=1なので、8×1=8
となります、双方を掛け合わせた時の数値が比例定数になる関係のことを反比例といいます。
最後に

比例、反比例というのは、中学・高校の数学でも使われるものなので、小学生のうちに仕組みやイメージをしっかり理解しておきましょう。
数値と数値の関係性のことなので、二つの数値がそれぞれ増えた時どのように変化しているかに着目して関係性を見抜きましょう。
勉強法としては、グラフが必要でない場合でも、何度か描いてみると比例・反比例をイメージしやすいかもしれません。



