中学2年生の数学では、「図形の調べ方」と「図形の性質と証明」という単元で図形を勉強することとなります。
図形問題が苦手という声も多く聞きますが、いくつか図形について覚えておけば簡単に解ける問題も多いのでしっかりと基礎を身につける必要があります。
そこで、この記事では「図形の調べ方」と「図形の性質と証明」の基礎を解説していきます。
図形の調べ方
それではまず「図形の調べ方」で学習する内容について、覚えておくべき基礎情報を紹介していきます。
対頂角の性質
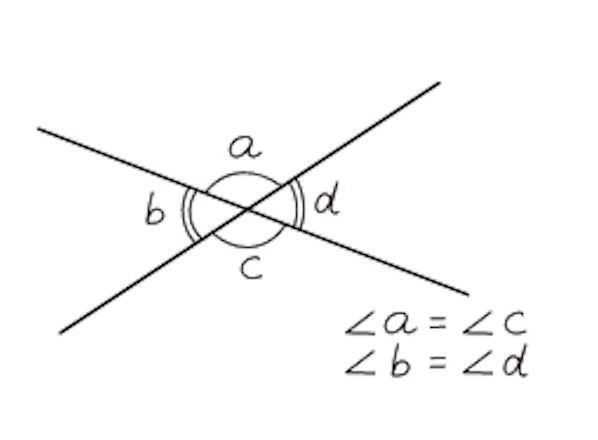
2つの直線が交わってできる4つの角のうち、右の図の∠bと∠dのような位置にある2つの角を対頂角(たいちょうかく)といいます。
対頂角には以下の性質があります。
- 対頂角は等しい
は等しいという性質を持ち、上の図を元にみると∠a = ∠c、∠b= ∠dであることがわかります。
平行線と角
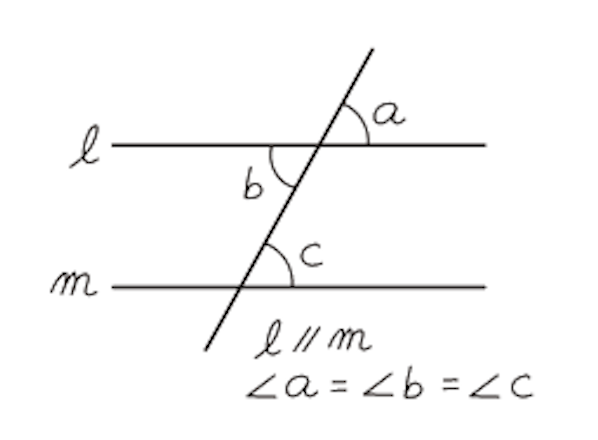
2直線を横切るようにもうひとつの直線が交わるとき、8つの角が上の図のようにできると思います。
このとき、∠a と∠cのように同じ位置にある2つの角を同位角といい、また、∠b と∠c のように、2直線の内側にある2つの角を錯角といいます。
そしてそれぞれ以下のような性質を持っています。
- 2つの直線が平行ならば、同位角は等しい。
- 2つの直線が平行ならば、錯覚は等しい。
上の図の場合∠a と ∠cは同位角で等しく、∠bと∠cは錯覚で等しいので、つまり∠a =∠b=∠cとなります。
三角形の内角・外角
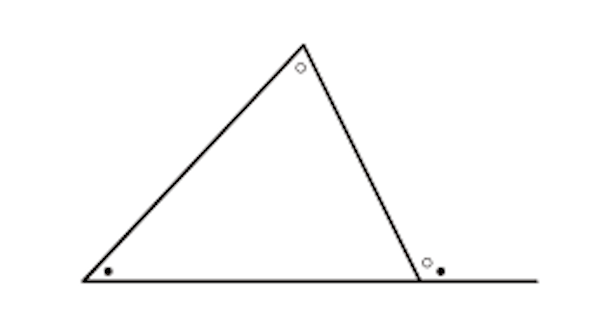
内角とは図形の内側の角のことです。
外角とは、内角と隣り合った角のことで、上の図でいう「○●」のような角を指します。
それぞれ内角と外角は以下の性質を持ちます。
- 三角形の内角の和は180°である。
- 三角形の1つの外角は、そのとなりにない2つの内角の和に等しい。
多角形の内角の和
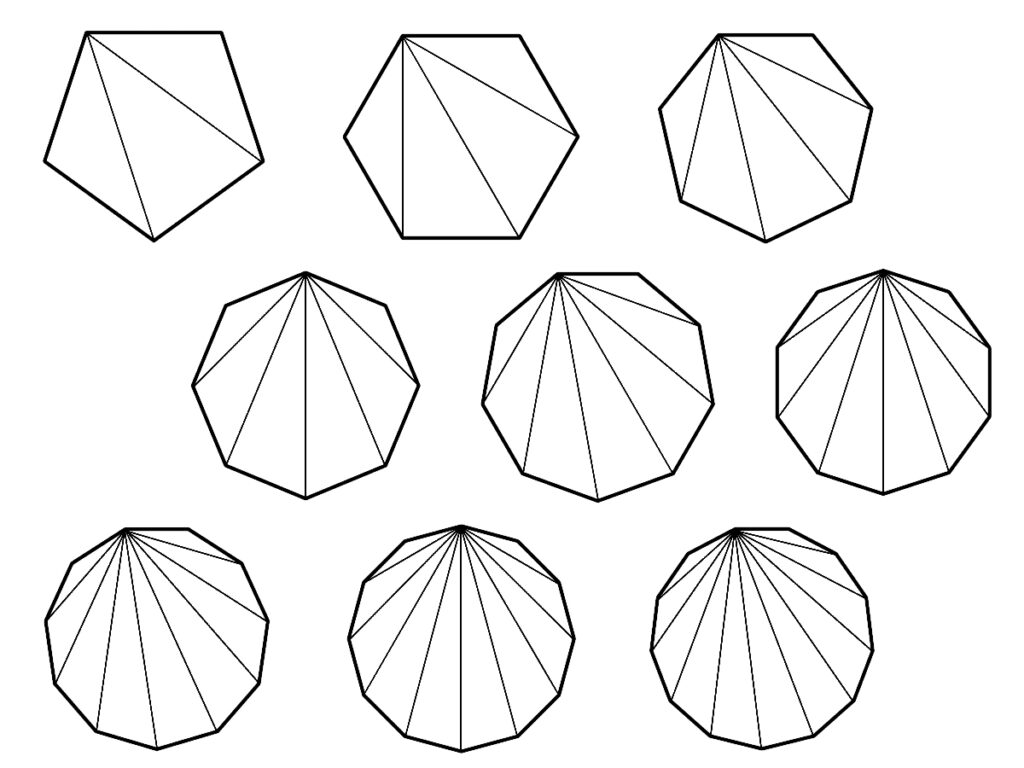
多角形のの内角は上の図のように、三角形に分解することができます。
これは○角形の○-2をした数の三角形に分割することができるため、以下の計算で求めることができます。
- (nー2)×180 °
合同な図形の性質
2つの図形が、その図形の位置や向きをかえるだけで、形と大きさをかえずに一致させることができる場合、その2つの図形は 合同であるといいます。
合同な図形には以下のような性質があります。
- 合同な図形で、対応する線分の長さはそれぞれ等しい。
- 合同な図形で、対応する角の大きさはそれぞれ等しい。
また、合同の時≡という記号を用いることで記述可能で、三角形三角形ABCと三角形DEFが合同の場合は「△ABC ≡ △DEF」と記すことができます。
三角形の合同条件
2つの図形が合同であるために、満たすべき条件を 合同条件といいます。
2つの三角形の合同条件は以下の3つで、いずれかを満たす場合に、合同です。
- 3組の辺がそれぞれ等しい場合
- 2組の辺とその間の角がそれぞれ等しい場合
- 1組の辺とその両端の角がそれぞれ等しい場合
2つの三角形が合同であることを証明する場合は以下の手順で行います。
①どの2つの三角形が合同であることを示すのか説明
②仮定や図形の性質から等しいといえる辺や角を説明
③三角形の合同条件のどれを使うのかを説明
④結論を書く
図形の性質と証明

「図形の性質と証明」では、図形の性質を証明するという問題を解くことになります。
証明とは、すでに成り立つことがわかっていることを使って、成り立つかどうかわからないことが実は成り立つということを確かめることの内容について説明することです。
記述問題を解く上では絶対に知っておかなければならない図形の性質があるので、みていきましょう。
二等辺三角形の性質と証明
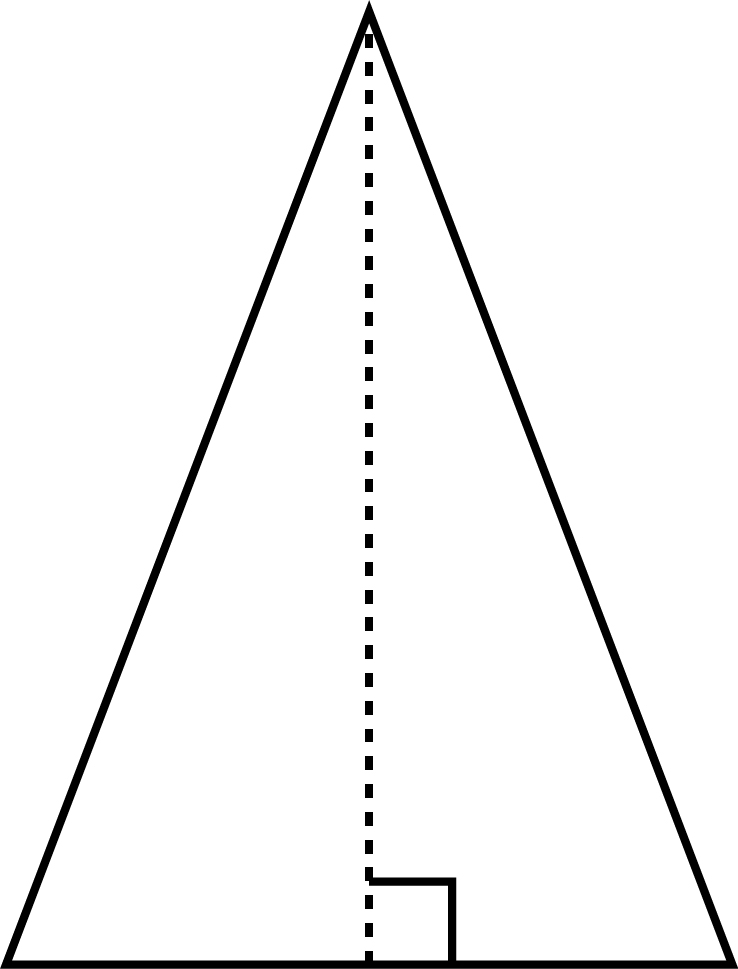
2つの辺が等しい三角形を二等辺三角形といいます。上の図のように二等辺三角形では,等しい辺の作る角を頂角,頂角に対する辺を底辺,底辺の両端の角を底角といいます。
この二等辺三角形には以下の性質があります。
- 二等辺三角形の2つの底角は等しい
- 二等辺三角形の頂角の二等分線は、底辺を垂直に2等分する
そのため、次の条件が成り立つとき,三角形は二等辺三角形になります。
- 三角形の2つの辺が等しい
- 三角形の2つの角が等しい
これらを使って問題を解くことができます。
正三角形の合同の性質と証明
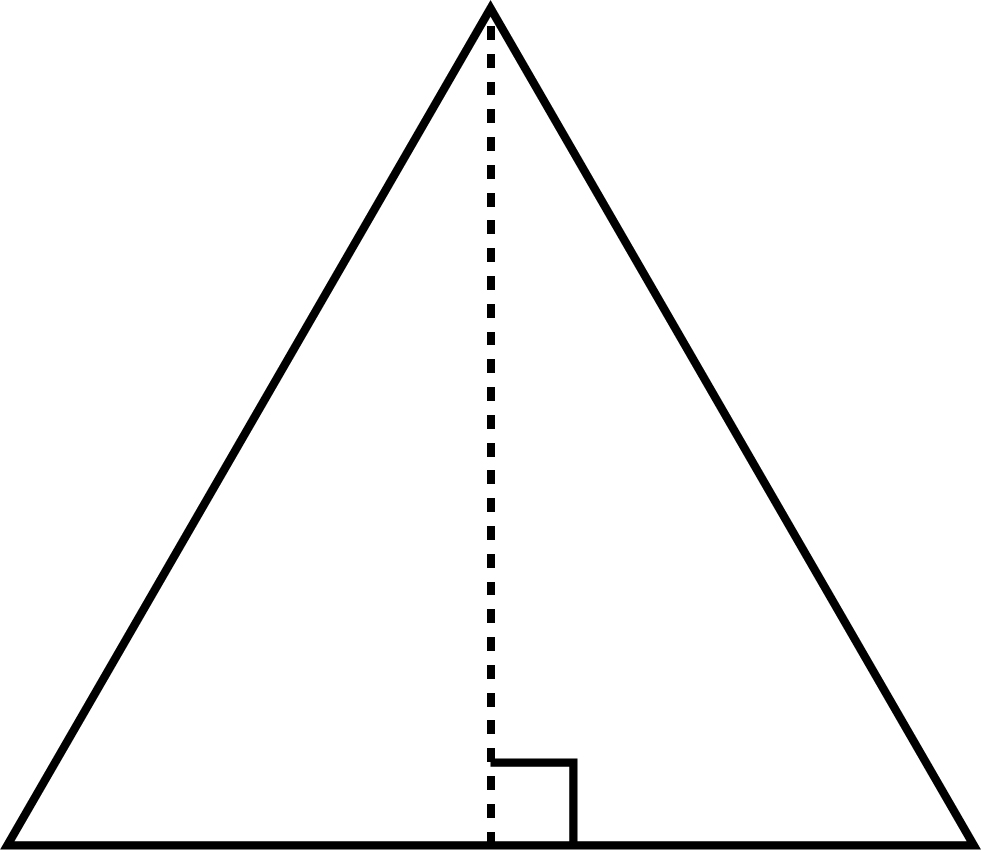
3つの辺がすべて等しい三角形を正三角形といいます。
また、3つの辺がすべて等しいということは言い換えると、「2つの辺が等しい三角形」ということもでき,二等辺三角形とも言えるでしょう。
そのことから,次の二等辺三角形の定理は,正三角形においても成り立つことになります。
また,正三角形には次の性質があります。
- 正三角形の3つの内角は等しい(60度)
最後に

「図形の調べ方」と「図形の性質と証明」では、図形に関する知識をしっかりと頭に入れないと解けない問題が多いです。
そのため、しっかりと図形の性質について理解し、証明問題に関しては、合同条件についてもしっかりと頭に入れ込みましょう。
頭に入れたらあとはひたすら問題演習をしていくことで解けるようになります。



