中学2年生の理科では、「電気・磁石-回路」という単元を学習します。
そこでこの記事では、この単元が苦手という中学生やそして中学生に勉強を教える親御さんのために抑えておくべき重要なポイントをわかりやすくまとめたので参考にしてください。
回路図の書き方をマスターしよう!
電流が通る道すじを「回路」といいます。
回路に1ヶ所でも切れ目があると電流は流れないので、回路は必ず切れ目なくつながっています。
この回路を電気用図記号をつかって表した図を回路図といいます。
回路図を書く時は以下の3つのポイントを守っていれば簡単に書くことができるのでぜひマスターしましょう。
- 導線は直線で書く電気器具は電気要図記号を使って書く導線の曲がり角は90
- 度導線の交わりには点を書く
- 導線の角には電気器具を書かない
直列回路と並列回路の違い
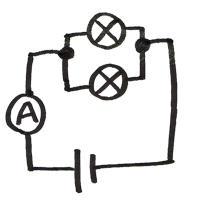
直列回路と並列回路の違いはしっかり押さえましょう。
まずはそれぞれの回路の説明を見てみましょう。
直列回路…電流の流れる道すじが1本道になっている回路
並列回路…電流の流れる道すじが枝分かれしている回路
この2種類の回路の違いは、導線の道筋の数です。
もし、導線の道筋が1本で繋がっているなら直列回路、1本じゃなくて2本以上ならば並列回路となります。
直列回路と並列回路の見分け方
回路の道筋を一筆書きできるかどうかで直列回路と並列回路の見分けることができます。
一筆書きで回路の道筋をかけた場合は直列回路
一筆でかけない場合は並列回路となります。
電流の性質
覚えるべき電流の性質をまとめました。
- 電流とは回路を流れる電気の量が電流の大きさ
- 1000mA=1A
- 電流の大きさは、枝分かれしなければどこでも等しい
- 枝分かれする場合、枝分かれした電流の大きさの和が分かれる前の電流の大きさに等しい
- 回路を流れる電流の強さは電流計ではかる。
電流計の使い方
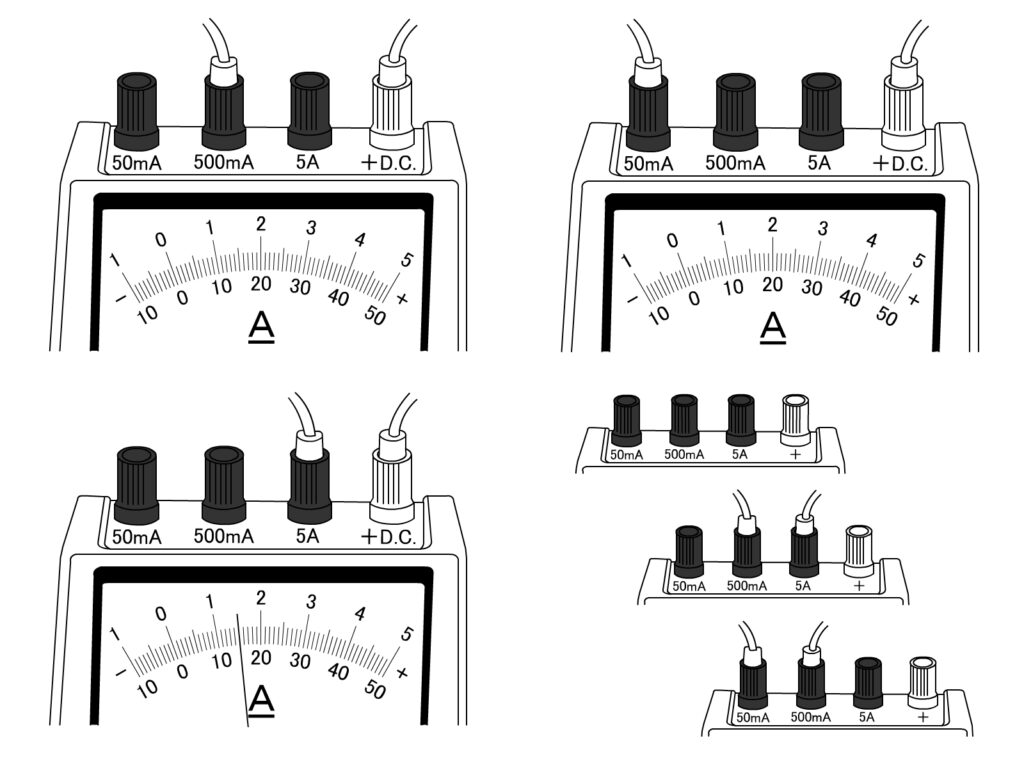
電流計を回路に直列につなぎ、電源の+極側の導線を電流計の+端子に、-極側の導線を-端子につなぎ、目盛りを読むだけです。
-端子の50mAは50mAまで、500mAは500mAまで、5Aは5Aまではかることができますが、電流の強さが予想できない場合は、5Aの-端子につなぎ、 指針の振れが小さいときは、-端子をつなぎかえます。
電圧の性質
覚えるべき電圧の性質を以下にまとめました。
- 電圧とは電気を流そうとするはたらきの大きさ
- 単位はV(ボルト)である。
- 電圧は並列では等しく、直列では和になる。
電圧計の使い方
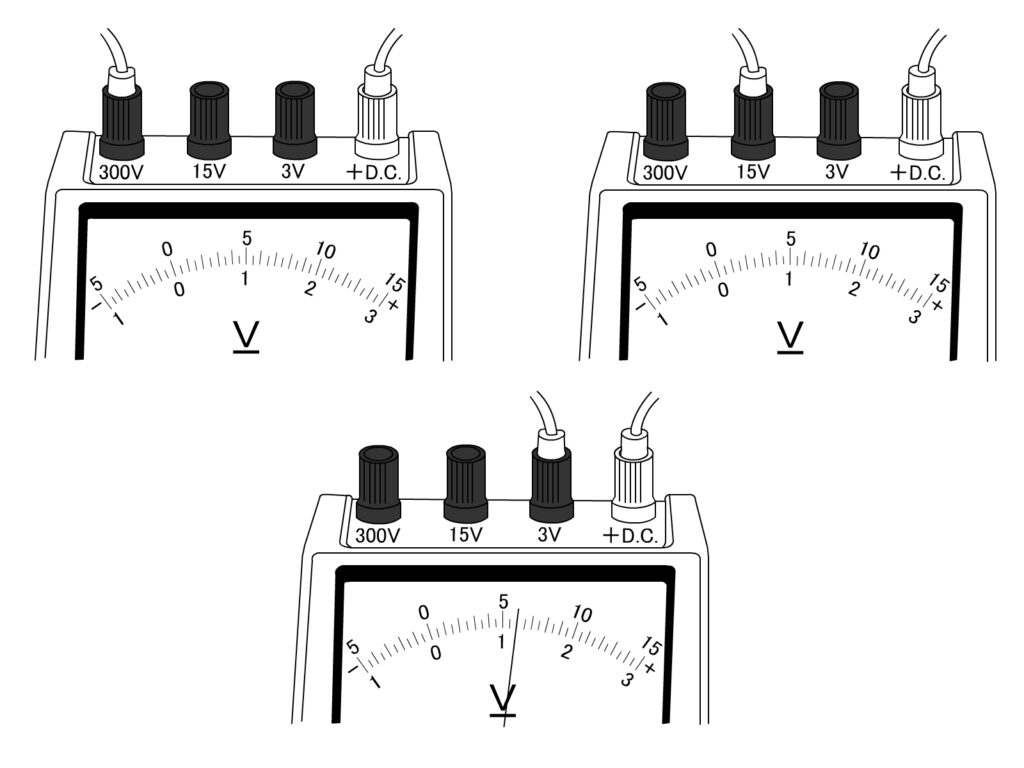
電圧は並列では等しく、直列では和になるため、電圧計ははかりたいところに並列につないで使います。
電圧の大きさが予想できない場合、−端子は最も大きい300Vにつないで使います。
直列回路の電圧・電流・抵抗の求め方
最後に直列回路と並列回路のの電圧・電流・抵抗の求め方をまとめたので、しっかり計算方法を覚えましょう。
まずは直列回路です。
直列回路の電流の求め方
直列回路は枝分かれしないので、電流はどの部分でもすべて同じ値になる。
つまり、どこかの地点での電流がわかればそのまま同じで良いということです。
直列回路の電圧の求め方
電圧は抵抗にかかる電圧の和が電源の電圧に等しいという性質から求めることがでできます。
電圧の和が電源電圧になるということは、電源電圧と他の抵抗がわかっていれば求めることができますね。
直列回路の抵抗の求め方
回路全体の抵抗は、それぞれの抵抗を足したものに等しいつまり、直列回路だったら抵抗値をたすと全体の抵抗が求められます。
並列回路の電圧・電流・抵抗の求め方
続いては並列回路の場合です。
並列回路の電圧の求め方
抵抗が並列つなぎでつながっていると加わる電圧が等しいという性質から求めることができます。
並列回路では各抵抗にかかる電圧は電源電圧と等しいので、電源電圧さえわかっていればそのままそれが並列回路の電圧になります。
並列回路の電流の求め方
枝分かれする回路では、電流は各枝に別れて流れるので別れた後の電流の和が、別れる前の電流と等しくなるという性質を持っています。
つまり、枝分かれの電流を足したら、全体の電流になるという求め方ができます。
並列回路の抵抗の求め方
全体の抵抗の逆数は各抵抗にかかる抵抗の逆数を足したものに等しいというルールがあります。
例えば、2つの抵抗が並列回路で繋がっていて、抵抗Aが100Ω、抵抗Bが200Ωだとした時に2つの抵抗を合わせた全体の抵抗値を求めたいとします。
先ほどのルールを式に表すと以下のような計算式が成り立ちます。
(Aの抵抗値)分の1 +(Bの抵抗値)分の1 = (全体の抵抗値)分の1
これを計算していくと、
100分の1 + 200分の1 = (全体の抵抗値)分の1
200分の3 = (全体の抵抗値)分の1
(全体の抵抗値)= 200/3 ≒ 66.6666Ω
と全体の抵抗値が求めることができるということです。


